Sommaire
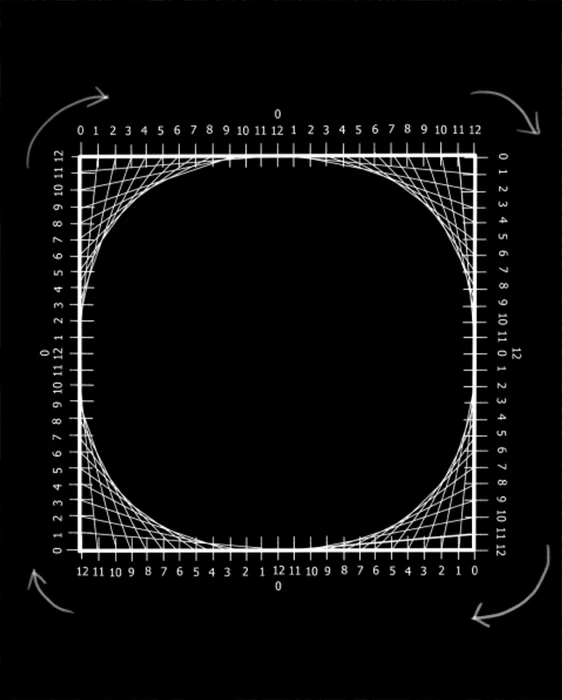
Une enveloppe graphique se crée en déplaçant une ligne selon une règle précise. Ce mouvement génère une courbe élégante qui relie toutes les positions successives de la ligne. Lorsqu’on l’applique à un carré, la ligne glisse le long de ses côtés, pivotant autour de chaque coin. Cette méthode offre une manière ludique d’explorer les formes géométriques, captivant ainsi l’imagination des plus jeunes. Elle permet aussi de stimuler la créativité, idéale pour débuter en string art. Dans cet article, nous vous guiderons pour construire une enveloppe carré avec un carré de 12 cm.
Résumé de l'article :
Pour réaliser notre figure, il faut:
Le matériel : un crayon, une gomme, une regle graduée et une feuille.
Première étape: Dessiner un carré
Deuxième étape : Graduer et orienter le carré.
Troisième étape : Comprendre le processus de base
Quatrième étape : Reproduire le processus dans le carré.
1 - Le matériel adéquat pour le carré
Que vous soyez un amateur de papier et crayon ou une personne passionnée d’informatique, une multitude d’outils est disponible pour vous. Pour une méthode manuelle, il est simple de tracer votre carré (enveloppe) en utilisant un simple crayon, une gomme, une règle graduée et une feuille. Si vous privilégiez la précision et le dévouement, des logiciels de dessin tels qu’Illustrator, Photoshop, Clip Studio ou Inkscape proposent une large sélection d’options. De plus, des logiciels de géométrie dynamique comme GeoGebra ou Cabri permettent d’observer les transformations en temps réel et d’approfondir la compréhension des notions mathématiques. Finalement, l’utilisation d’outils tels que Python (matplotlib) ou Processing dans le domaine de la programmation permet d’obtenir des créations singulières et fortement personnalisées.
2 - Réalisation du carré
... Etape 1: Dessiner un carré de 12 cm
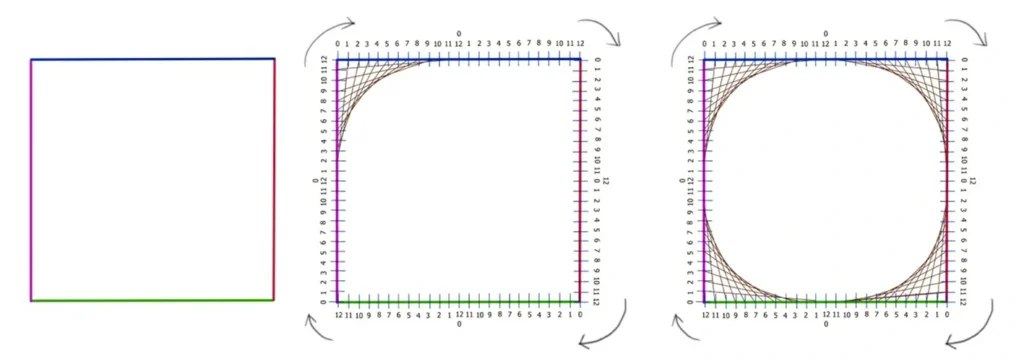
Pour débuter cette tâche, il est crucial de tracer un carré. Cette figure a été sélectionnée de manière judicieuse, car sa régularité facilite les premières constructions tout en précisant les étapes. Grâce à ses côtés de 12 centimètres, le carré sera simple d’utilisation pour nos exercices. Pour optimiser la compréhension, il est possible de colorer les quatres côtés en différentes teintes ou de notter ses cotés avec A, B, C et D. Qu’elles soient effectuées manuellement ou avec des outils numériques, ces conseils visuels facilitent la compréhension des prochaines étapes.
... Etape 2: Graduer le carré
Après avoir tracé notre carré, nous procéderons à sa graduation. Sur chaque côté, disposons 24 points équidistants que nous identifierons de 0 à 12, en fonction des milieux des côtés de ce carré. De plus, une distance de 0,5 cm est laissée entre deux divisions. Par ailleurs, pour tous les côtés du triangle, il est crucial de choisir un sens de parcours. Par exemple, on peut choisir de déplacer le carré depuis la droite vers la gauche.
... Etape 3: comprendre le processus de base
Notre enveloppe va progressivement se tracer. Répétons cette action simple : Débutons par connecter les points de numéro identique sur les côtés rouge et violet : 1 avec 1, 2 avec 2, 3 avec 3, etc., jusqu’à atteindre 12 avec 12. Il s’agit d’assembler les pièces d’un puzzle, mais en utilisant des lignes !
... Etape 4: Reproduire le processus dans le carré
Répétons le processus : Relions les points associés sur les côtés consécutifs : bleu et rouge, puis sur les côtés suivants : rouge et vert, pour finalement se terminer par vert et violet. Il est crucial de respecter le sens de parcours défini au départ pour ne pas s’embrouiller. À chaque étape, l’enveloppe se forme, les segments se reliant comme des pièces d’un puzzle.
3 - Exercices autour du carré
Pour enrichir nos découvertes géométriques, pourquoi ne pas apporter une touche de fantaisie ? Prenons l’exemple de notre carré, mais pour une seconde fois, il mesure 20 cm de long. En effet, en reliant les points, il serait possible de concevoir des motifs encore plus complexes. De plus, il est possible de dépasser les sentiers battus en testant avec des rectangles. Des rectangles dont la longueur serait deux fois supérieure à la largeur ? Il y a des possibilités sans fin ! Par ailleurs, pour une note unique, employons des teintes diversifiées ou même des fils enroulés sur un support en bois. Par conséquent, la géométrie se transforme en un espace de jeu où l’imagination ne rencontre plus d’obstacles. Donc, êtes-vous prêts à découvrir de nouvelles perspectives créatives ?
4 - Des Enveloppes et des Formes :
On peut concevoir des courbes complexes et captivantes en utilisant des formes basiques comme le triangle, le carré ou le cercle. Un univers rempli de notions géométriques comme la rotation, la tangence ou le concept de l’enveloppe en elle-même se dissimule derrière chaque enveloppe. Cette activité ne se limite pas à un simple plaisir, elle transforme des concepts abstraits en réalités concrètes, rendant les mathématiques plus séduisantes. De plus, la variété des formes possibles et le design esthétique des résultats font de cette méthode un véritable catalyseur pour l’imagination. Qu’il s’agisse de papier, de logiciels comme GeoGebra ou d’outils plus conventionnels, la découverte des enveloppes permet d’accéder à un monde mathématique fascinant et sans fin.
Tu as aimé cet article utile ? Aime et partage le avec d’autres personnes !
Galerie d’art numérique…
L’art numérique, né des avancées technologiques, a transformé les scènes artistiques mondiales. Cépendant, si l’Occident a été pionnier, l’Afrique, notamment…
Hadassa Ngamba :…
Hadassa Ngamba, artiste visuelle congolaise née en 1993, explore la mémoire coloniale du Congo à travers un travail multidisciplinaire. Profondément…
L’Art NFT au…
Le Cameroun, riche en art et culture, s’engage dans une évolution artistique passionnante. L’essor de l’art NFT transforme son paysage…
Auteur
Je m’appelle Mba Verlaine, une artiste camerounaise passionnée par la culture africaine. Sur ce blog, je partage régulièrement mes réflexions et mes découvertes sur les arts, les traditions et les sujets qui me tiennent à cœur.
